平均から分位点へ：分位点回帰

過去のブログエントリにおいて、
「高学歴ほど収入の振れ幅が大きい」とのお話がありました。
以下の論文は、回帰分析でその問いに答える研究をしています。

Angrist,Chernozhukov, and Fernandez-Val (2006) “Quantile Regression Under Misspecification, with an Application to the U.S. Wage Structure”

ではこの論文ではどのように分析したのでしょうか。
今回は分位点回帰(Quantile Regression)のご紹介です。

振れ幅が大きくなる現象をどう捉えるか

収入の振れ幅が大きいとは格差が大きいということなので、
データがより広く散らばっていることになります。
言い換えると、分散が大きくなっていることになります。

つまり学歴が高くなるにつれて、
分散が大きくなることを確認すればよいことになります。
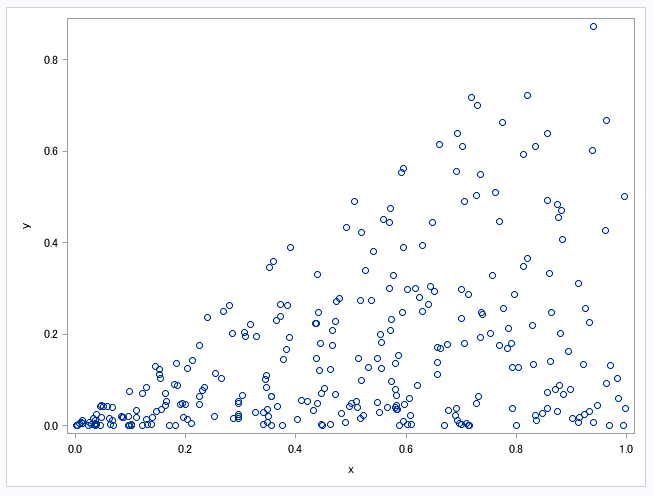
単回帰分析であれば以下のように散布図を作成すれば、容易に確認できます。

しかし、現実ではそうは簡単にいきません。
例えば重回帰分析の場合、散布図では確認することはできません。
では、どのようにすれば分析できるでしょうか。

分位点で回帰する分位点回帰(Quantile Regression)

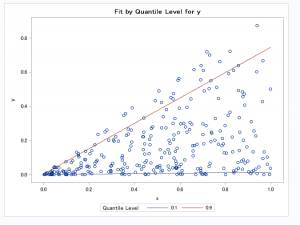
上の散布図において、
x(横軸)ごとのy(縦軸)の最小値付近を対象にすると、傾きはゼロになります。
対してxごとのyの最大値付近をみると、恐らく傾きは1程度になるでしょう。

例えば、yの分布の両端を対象にそれぞれ回帰直線を引くと、
以下のような 線になります。

つまり格差が拡大するケースでは、
分位点が最大値に近づくにつれて、傾きが大きくなるはずです。
このように平均ではなく、分位点を用いた回帰分析を、
分位点回帰(Quantile Regression)といいます。

種明かしをしますと、上の図における直線は
90%と10%のそれぞれの分位点で
分位点回帰を実行した回帰直線です。

この2つの回帰直線の傾きの差が大きいほど、
格差が拡大していくということになります。

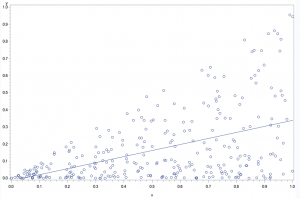
ちなみに通常の回帰直線はこんな感じです。
違いがお分かり頂けたでしょうか。

ここまでのまとめ

・ 分位点回帰は平均以外の分布の切り口を使って回帰分析ができる

・ 説明変数(横軸の変数)の値によって被説明変数(縦軸の変数)の格差が拡大
　することを見たい場合：
　　　　　　　↓
　分布の両端(例えば10%と90%の分位点)で分位点回帰を行い、傾きの差を見る。

話を戻すと…

話を戻しますと、今回のエントリの目的は、
「高学歴ほど収入の振れ幅が大きい」ことを検証することにあります。

つまり収入と学歴の関係が、
上の散布図のようになっていればよいことになります。
しかし、現実では他の要素も関係してくるので、
分位点回帰で分析してみましょう。

使用データ

まずはデータから。今回使用するデータは、
Angrist, Chernozhukov, and Fernandez-Val (2006)で使用されているデータです。
このデータは2000年、1990年、1980年にアメリカで行われたセンサスデータの一部です。

データは以下のURLからダウンロードできます。

http://economics.mit.edu/faculty/angrist/data1/data/angchefer06

早速データをインポートしましょう。


proc import datafile='C:\usr\usrname\folder\angcherfer06\Data\census00.dta'
out =work.census
dbms=dta replace;
run;


Angrist, Chernozhukov, and Fernandez-Val (2006)では、
分析に用いた変数は賃金と教育年数のみでしたが、他の変数も使用してみましょう。
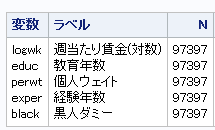
今回は以下の変数を使用します。

今回は2000年のデータを用いて、分位点回帰を実行しましょう。
SAS/STATのquantregプロシジャで実行できます。
分位点はmodelステートメントのq=オプションで指定します。

今回は10%、25%、50%、75%、90%の分位点で実行します。

ちなみに50%分位点は、
メディアンを使った「最小絶対偏差推定(Least Absolute Deviation Estimation:LAD推定)」です。


proc quantreg data = census ;
model logwk = educ exper black / quantile =.1 .25 .5 .75 .9;
weight perwt ;
run ;


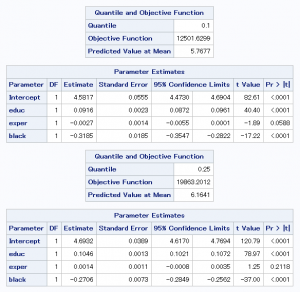
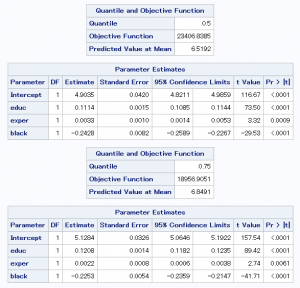
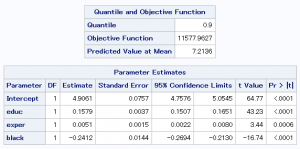
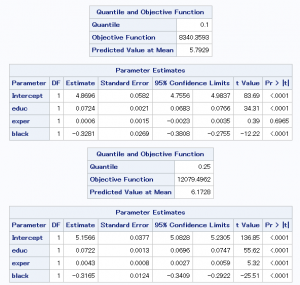
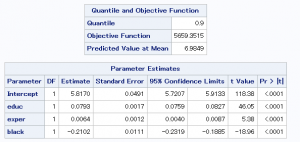
結果出力中の「Quantile and Onjective Function」の表にあるQuantileの項目が分位点を表しています。
上から10%、25%、50%、75%、90%の順番で表示しています。

教育年数(educ)に注目してみると、分位点が最大値に近づくにつれ、
傾きが大きくなっていることが分かります。
従って、学歴が高くなるにつれ、
収入の格差が拡大するという仮説を支持する結果であると言えます。
それでは80年のデータを使うと、どのような結果になるでしょうか。


proc import datafile='C:\usr\usrname\folder\angcherfer06\Data\census80.dta'
out =work.census
dbms=dta replace;
run;

proc quantreg data = census80 ;
model logwk = educ exper black / quantile =.1 .25 .5 .75 .9;
weight perwt ;
run ;

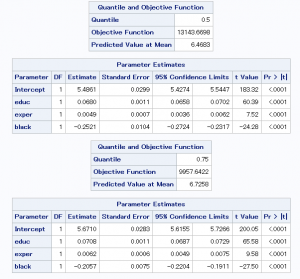
この結果をみると、10%と90%の分位点における傾きの差は、
2000年に比べて小さいことが分かります。
つまり20年の間に労働市場の構造が変化したことになります。

また、2時点間において黒人ダミー(black)の係数値にあまり変化が見られません。
人種による収入の格差が如何に根深いかが伺えます。

分位点回帰のメリット

最後に分移転回帰のメリットを2点挙げます。
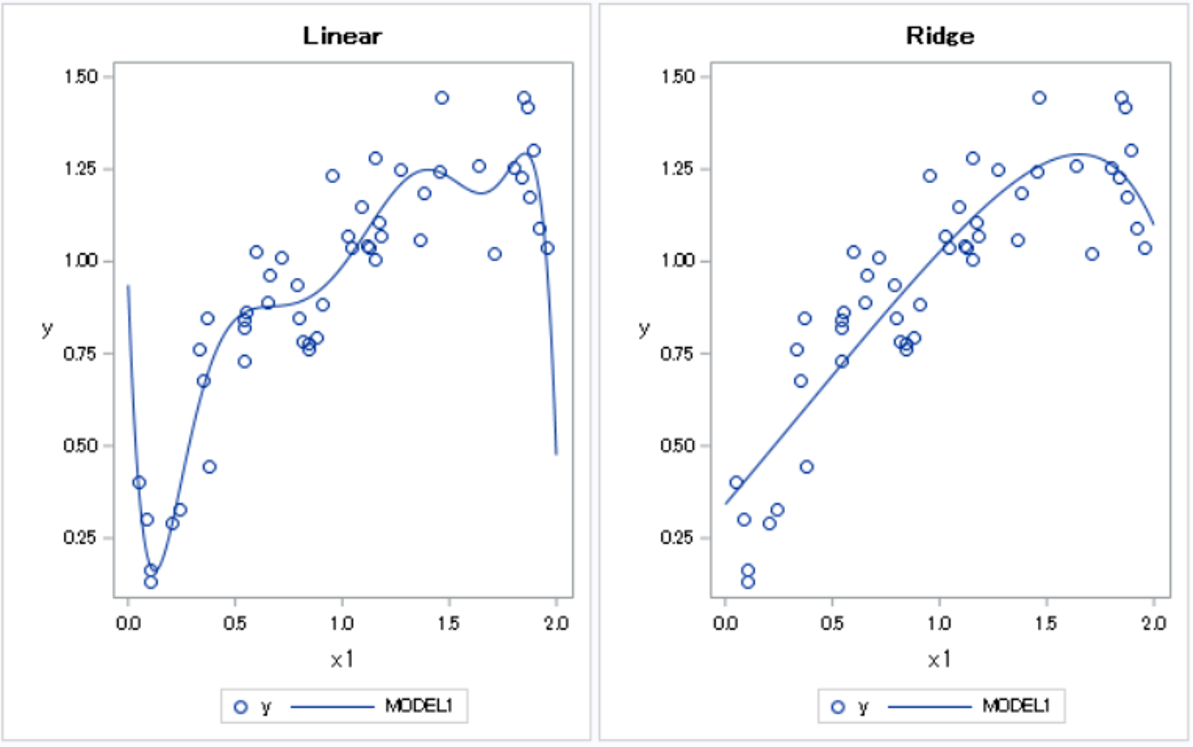
1．外れ値に依存しない
最小二乗法は平均値を用いるため、外れ値に大きな影響を受けます。
一方で分位点回帰は、メディアンなどの分位点を用いるため、外れ値に影響されにくくなります。

2.分布の形の変化を掴むことができる
分位点ごとの回帰を行うことで、説明変数の値の変化と共に、
被説明変数の分布の形がどう変化するかを分析することができます。
今回の投稿ではこちらのメリットを活用しました。

今回は理論的な部分には触れませんでしたが、
基本的な理論とその応用については以下の本がおすすめです(訳本もあります)。


Mostly Harmless Econometrics: An Empiricist's Companion
(邦題：「ほとんど無害」な計量経済学―応用経済学のための実証分析ガイド)
著者：Joshua Angrist and Jörn-Steffen Pischke